Xét một bàn cờ vua có kích thước \(m \times n\) gồm có \(m\) dòng, \(n\) cột. Các dòng được đánh số từ \(1\) đến \(m\), các cột được đánh số từ \(1\) đến \(n\). Một ô nằm trên dòng \(x\), cột \(y\) được kí hiệu là \((x,y)\)

Một quân mã xuất phát từ một ô trên bàn cờ có thể đi đến một trong bốn ô như hình vẽ.

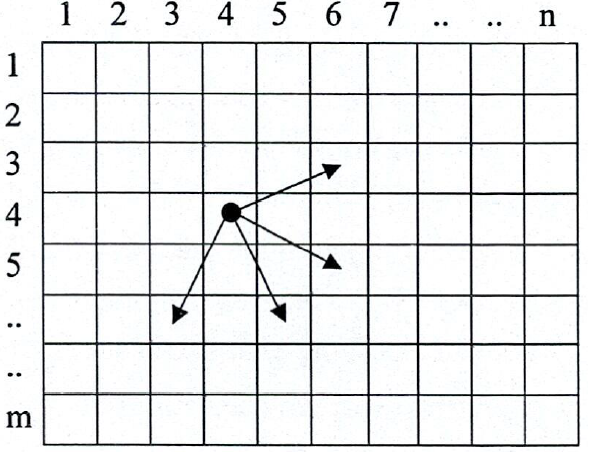
Ngoài ra, trên bàn cờ có \(k\) ô mà quân mã không được phép đi vào. Những ô này được gọi là ô bị cấm.

Yêu cầu:

• Tìm số cách di chuyển của quân mã từ ô \((x,y)\) cho trước đến ô \((m,n)\).

Dữ liệu vào

• Dòng đầu tiên ghi \(4\) số nguyên \(m,n,k\) và \(Q\) \((1 \lt m,n \le 10^3; 0 \le k \lt 10); Q \le 10\)
• Trên \(k\) dòng tiếp theo, mỗi dòng ghi \(2\) số nguyên \(k_{x_i}, k_{y_i}\) cho biết ô \((k_{x_i},k_{y_i})\) bị cấm \((1 \lt k_x \lt m; 1 \lt k_y \lt n)\)
• Trên \(Q\) dòng tiếp theo, mỗi dòng ghi \(2\) số nguyên \(X_i,Y_i\) \((1 \le x_i \lt m; 1 \le y_i \lt n)\)

Dữ liệu ra

• Gồm \(Q\) số nguyên \(W_i\), mỗi số trên một dòng cho biết số cách di chuyển quân mã từ ô \((X_i, Y_i)\) cho trước đến ô \((m,n)\). Trong đó \(W_i\) là phần dư của phép chia số cách quân mã di chuyển từ ô \((X_i,Y_i)\) cho trước đến ô \((m,n)\) cho \(10^9\)

Scoring

• 30% test ứng với 30% số điểm có \(1 \lt m,n \le 100; k=0; Q \le 10^2\)
• 20% test ứng với 20% số điểm có \(1 \lt m,n \le 100; 0 \lt k \le 10; Q \le 10^2\)
• 50% test ứng với 50% số điểm còn lại có ràng buộc như đề bài.

Input 1

4 5 1 3 
2 4
1 3
3 3
2 4

Output 1

0
1
0

Input 2

4 5 0 2
1 2
3 3

Output 2

2 
1