Tam giác (THT-B-2022 Quảng Bình -Bắc Ninh -Nghệ An)
Xem dưới dạng PDFTrên mặt phẳng tọa độ có \(n+1\) điểm: điểm nguyên \(A(x,y)\) và \(n\) điểm nguyên nằm trên trục \(B_1(x_1, 0), B_2(x_2, 0),..., B_n(x_n,0)\).
Yêu cầu: Với số nguyên không âm \(S\), hãy đếm số lượng tam giác có diện tích lớn hơn \(S\) mà ba đỉnh của tam giác là ba diểm trong \(n+1\) điểm đã cho.
Dữ liệu:
- Dòng đầu tiên chứa hai số nguyên \(n\) và \(S (2 \le n; 0 \le S \le 10^9)\)
- Dòng thứ hai chứa hai số nguyên dương \(x, y (x, y \le 10^9)\)
- Dòng thứ ba chứa \(n\) số nguyên dương \(x_1, x_2,..., x_n (x_i \le 10^9)\)
Kết quả: Ghi ra thiết bị ra chuẩn gồm một số nguyên là số lượng tam giác đếm được.
Ràng buộc:
- Có 25% số lượng test ứng với 25% số điểm có \(n=2\);
- Có 25% số lượng test khác ứng với 25% số điểm có \(n \le 2000\);
- Có 25% số lượng test khác ứng với 25% số điểm có \(n \le 2 \times 10^5\) và \(S=0\);
- Có 25% số lượng test còn lại ứng với 25% số điểm có \(n \le 2 \times 10^5\);
Input
5 3
3 5
1 2 5 7 8Output
8Giải thích
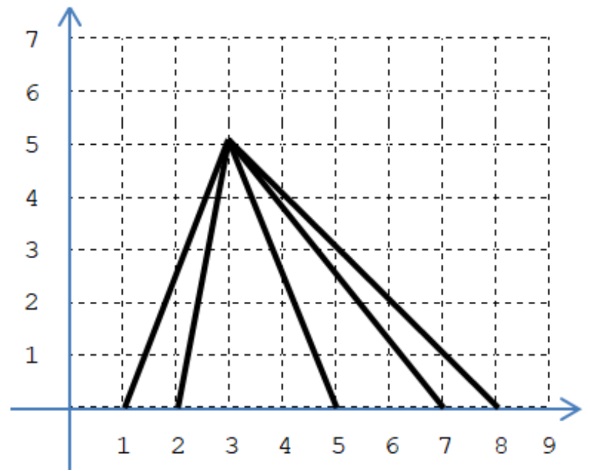
Nhận xét