Bản đồ thành phố \(X\) có dạng lưới ô vuông \(M\) hàng \(N\) cột. Các hàng được đánh số từ \(1\) tới \(M\), các cột được đánh số từ \(1\) tới \(N\). Mỗi ô vuông trên bản đồ có thể là khu đất trống, một khu dân cư hoặc một siêu thị.

Mỗi siêu thị chỉ có thể phục vụ các khu dân cư có khoảng cách so với nó không quá \(D\), nghĩa là nếu siêu thị nằm ở ô \((x, y)\) thì nó có thể phục vụ được tất cả các khu dân cư nằm trong hình vuông có tọa độ từ \((x - D, y - D)\) đến \((x + D, y + D)\).

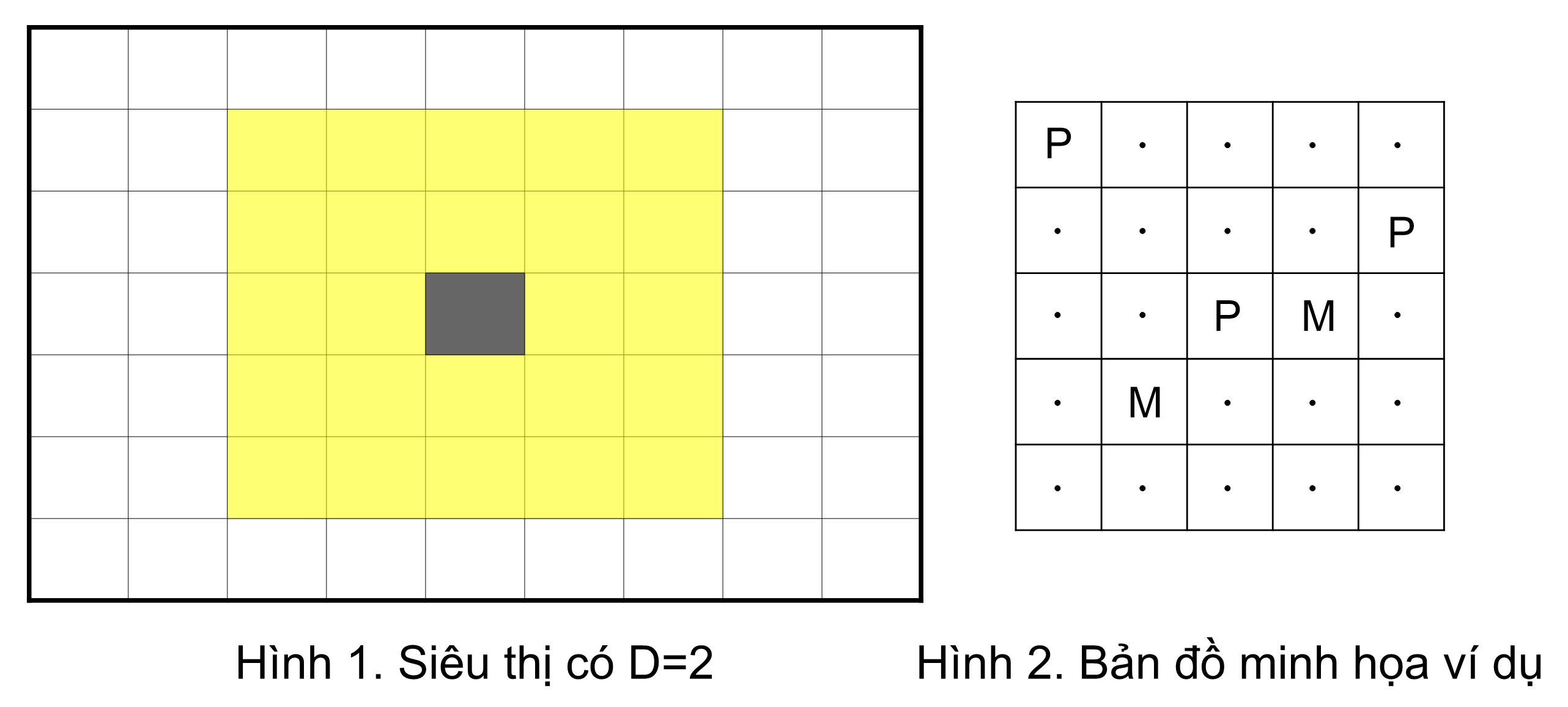
Một khu dân cư được gọi là "chất lượng cao" nếu được ít nhất \(K\) siêu thị có thể phục vụ. Cho biết bản đồ của thành phố \(X\), hãy đếm số lượng khu dân cư "chất lượng cao".

Dữ liệu vào

• Dòng đầu tiên chứa \(4\) số nguyên \(M, N, D\) và \(K\) (\(1 \le D \le max(M, N), 1 \le K \le M \times N\)).
• \(M\) dòng tiếp theo, mỗi dòng gồm \(N\) ký tự, mô tả bản đồ:
• Dấu chấm ('.') biểu diễn khu đất trống.
• Chữ 'P' biểu diễn khu dân cư.
• Chữ 'M' biểu diễn một siêu thị.
• Dữ liệu đảm bảo: Có ít nhất một khu dân cư và ít nhất một siêu thị.

Dữ liệu ra

• Ghi ra một số duy nhất là số khu dân cư "chất lượng cao".

Ràng buộc:

• 40% số test ứng với 40% số điểm: \(M = 1, N, D < 10^3\).
• 20% số test ứng với 20% số điểm: \(M = 1, N ≤ 10^5\).
• 20% số test khác ứng với 20% số điểm: \(2 ≤ M, N ≤ 10^3\), số khu dân cư và siêu thị không vượt quá \(10^3\).
• 20% số test còn lại ứng với 20% số điểm: \(2 ≤ M, N ≤ 10^3\).

Input 1

5 5 1 2
P....
....P
..PM.
.M...
.....

Output 1

1

Giải thích

Bản đồ minh họa như hình. Khu dân cư tại (1,1) không được siêu thị nào phục vụ. Khu dân cư tại (2,5) được một siêu thị phục vụ. Khu tại (3,3) được hai siêu thị phục vụ.