Consider a grid of size \(n \times n\) where each cell contains a number. Let's call a grid stable if we can rearrange the numbers of each row so that every column of the resulting grid has no repeated values.

Mathematically, say, we have a grid \(G\) of size \(n \times n\). We would like to permute the elements of each row \(G_i\) (\(1 \le i \le n\)) so that the resulting grid has the following property:

For every column \(j\), the values \(G_i,_j\) are all distinct for (\(1 \le i \le n\)).

As an example, consider a grid \(G\) of size \(4 \times 4\) as shown below:

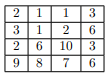
We can permute each row to get \(G'\) as shown below:

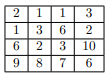
In this problem, you will be given a grid of size \(n \times n\) and you have to determine whether it is stable or not.

Input

Input starts with an integer \(T\) (\(\le 500\)), denoting the number of test cases. Each case starts with a line containing the value of \(n\) (\(0 \lt n \lt 100\)). The next \(n\) lines contain \(n\) integers each. The \(j\)-th integer of the \(i\)-th line represent the value of \(G_i,_j\) . Consecutive integers in each line are separated with space characters. All the integers in the grid are non-negative with magnitude not greater than \(100\).

Output

For each case, output the case number first. If the given grid is stable, output '\(yes\)' otherwise output '\(no\)'. Look at the samples for exact format.

Sample Input

3
4
2 1 1 3
3 1 2 6
2 6 10 3
9 8 7 6
3
1 1 2
1 1 1
2 2 2
3
1 2 3
2 3 1
3 1 2

Sample Output

Case 1: yes
Case 2: no
Case 3: yes