Trong một căn phòng hình chữ nhật kích thước 10 x 10, có:

• Cửa vào tại điểm \((0, 5)\)
• Cửa ra tại điểm \((10, 5)\)

Trong phòng có một số bức tường đứng (song song trục Oy). Mỗi bức tường:

• Có hoành độ cố định \(x\)
• Có hai lỗ trống cho phép đi qua:
  • Từ \(a_1\) đến \(b_1\)
  • Từ \(a_2\) đến \(b_2\)

Yêu cầu: tìm đường đi ngắn nhất từ điểm vào đến điểm ra, chỉ được đi xuyên tường qua các khoảng trống.

Định dạng vào

• Dòng đầu: một số nguyên \(n\) (\(n \le 20\)), là số tường.
• Tiếp theo \(n\) dòng, mỗi dòng gồm 5 số thực:
  • \(x, a_1, b_1, a_2, b_2\)

Các điều kiện:

• \(a_1 < b_1 < a_2 < b_2\)
• \(x_1 < x_2 < \dots < x_n\)

Định dạng ra

• Một số thực: độ dài đường đi ngắn nhất, làm tròn 2 chữ số sau dấu thập phân.

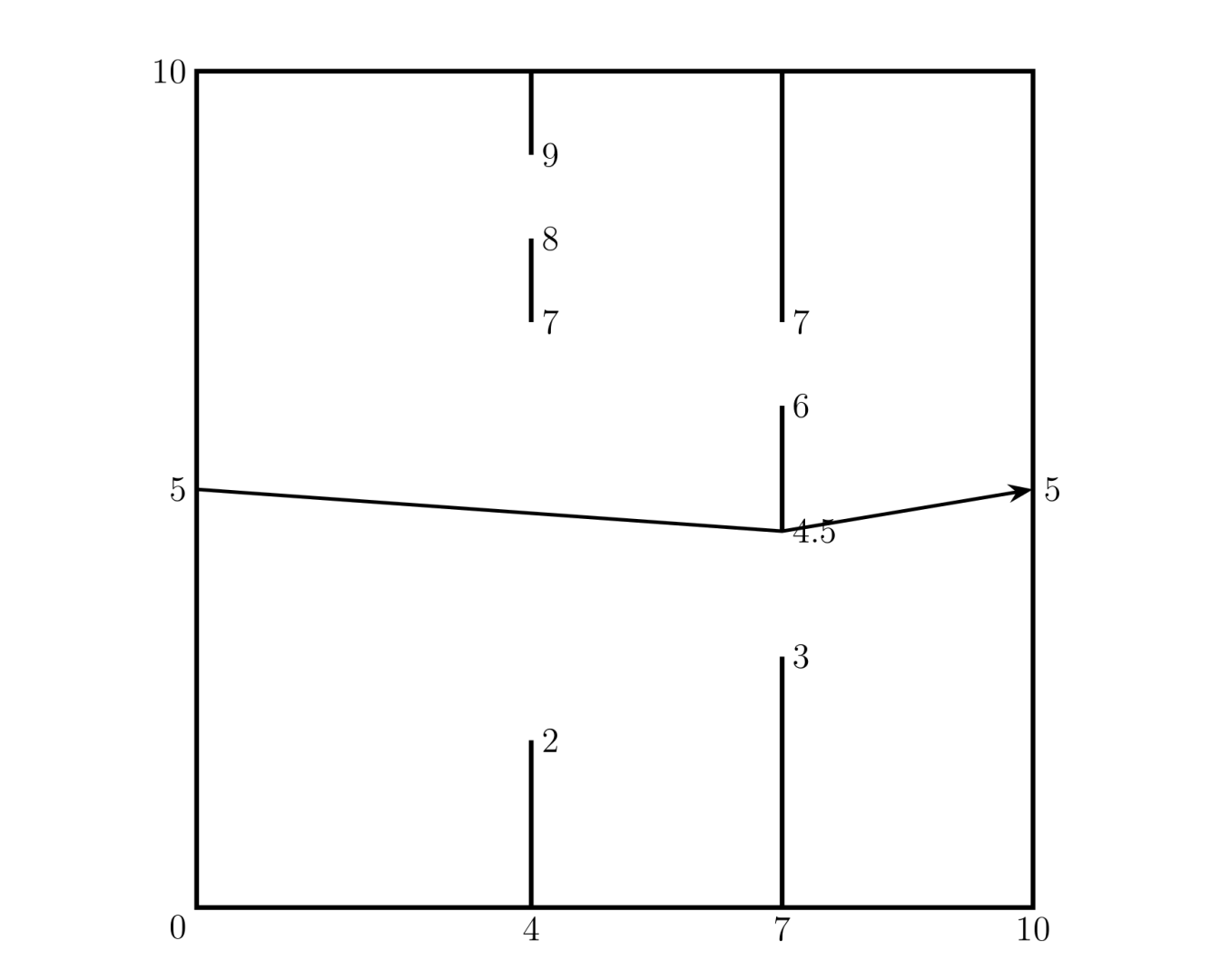
Input

2
4 2 7 8 9
7 3 4.5 6 7

Output

10.06

Gợi ý

• Mỗi lỗ trống sinh ra hai điểm đầu-cuối → có thể xem bài toán là tìm đường đi ngắn nhất trên đồ thị.
• Có thể sử dụng Dijkstra hoặc Floyd-Warshall trên tập hợp các điểm hợp lệ.