Một quân domino gồm hai phần: một ô trên và một ô dưới, mỗi ô có từ \(1\) đến \(6\) chấm.

Cho một dãy gồm \(n\) quân domino được đặt thành một hàng ngang. Với mỗi quân domino, số chấm ở ô trên và ô dưới được cho trước.

Gọi \(S_1\) là tổng số chấm của tất cả các ô phía trên, và \(S_2\) là tổng số chấm của tất cả các ô phía dưới.

Độ lệch giữa hai hàng chấm được định nghĩa là \(\left|S_1 - S_2\right|\).

Mỗi quân domino có thể được xoay \(180^\circ\) (tức đổi chỗ ô trên và ô dưới của nó). Hành động này thay đổi tổng điểm giữa hai hàng.

Yêu cầu

• Tìm số lần xoay domino tối thiểu để độ lệch \(\left|S_1 - S_2\right|\) là nhỏ nhất có thể.

Ví dụ minh hoạ:

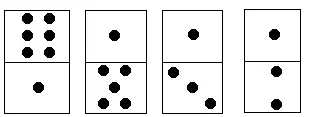
Trong ví dụ trên: \[ S_1 = 6+1+1+1 = 9,\quad S_2 = 1+5+3+2 = 11,\quad \left|S_1 - S_2\right| = 2 \]

• Chỉ cần xoay quân domino cuối cùng (1,2) thành (2,1), tổng điểm của hai hàng sẽ đều là 10, và độ lệch trở thành 0. Như vậy chỉ cần xoay 1 lần.

Dữ liệu vào

• Dòng đầu tiên là số nguyên \(n\) (\(1 \leq n \leq 1000\)) - số quân domino.
• \(n\) dòng tiếp theo, mỗi dòng gồm hai số nguyên \(a\) và \(b\) (\(1 \leq a, b \leq 6\)) - số chấm ở ô trên và ô dưới của một quân domino.

Dữ liệu ra

• Một số nguyên duy nhất - số lần xoay domino ít nhất cần thực hiện để độ lệch \(\left|S_1 - S_2\right|\) đạt giá trị nhỏ nhất.

Input 1

4
6 1
1 5
1 3
1 2

Output 1

1