Một lưới có thể cuộn theo cả chiều ngang và chiều dọc được gọi là torus. Với một torus mà mỗi ô chứa một số nguyên, nhiệm vụ là xác định hình chữ nhật con có tổng lớn nhất. Tổng của một hình chữ nhật con là tổng của tất cả các phần tử trong hình chữ nhật đó. Trong ví dụ dưới đây, một torus được minh họa với hình chữ nhật con có tổng lớn nhất được tô đậm.

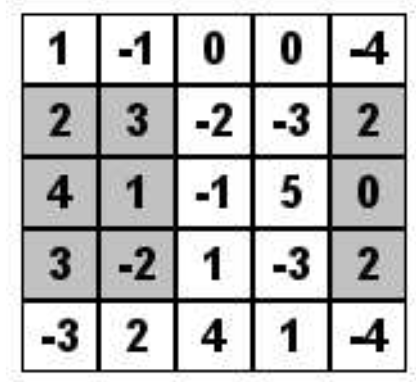
Dữ liệu vào

• Dòng đầu tiên chứa số lượng test \(t\) \((1 \le t \le 18)\)
• Mỗi bộ test sẽ bắt đầu là số nguyên \(N\) \((1 \le N \le 75)\) là kích thước của torus (hình vuông). \(N\) dòng tiếp theo, mỗi dòng chứa \(N\) số nguyên mang giá trị \(-100\) đến \(100\).

Dữ liệu ra

• \(t\) dòng, ứng với test bộ test, mỗi dòng là tổng lớn nhất tìm được

Input 1

2
5
1 -1 0 0 -4
2 3 -2 -3 2
4 1 -1 5 0
3 -2 1 -3 2
-3 2 4 1 -4
3
1 2 3
4 5 6
7 8 9

Output 1

15
45