Diện tích lớn nhất
Xem dưới dạng PDFCho \(n\) hình chữ nhật trong mặt phẳng \(2D\). Chọn một vùng được hình thành từ giao điểm của hai hình chữ nhật đã cho. Tìm diện tích lớn nhất của hình vuông có thể nằm gọn trong vùng này nếu bạn chọn vùng đó một cách tối ưu.
Input
- Dòng đầu là \(n\) số lượng hình chữ nhật
- \(n\) dòng tiếp theo, mỗi dòng chứa 4 số \(x_1, y_1, x_2, y_2\) là tọa độ \(x,y\) dưới cùng bên trái và trên cùng bên phải của hình chữ nhật thứ \(i\)
Output
- Diện tích lớn nhất có thể có của hình vuông hoặc \(0\) nếu không tồn tại bất kỳ vùng giao nhau nào giữa các hình chữ nhật.
Điều kiện
- \(2 \le n \le 10^3\)
- \(1 \le bottomLeft[i][0], bottomLeft[i][1] \le 10^7\)
- \(1 \le topRight[i][0], topRight[i][1] \le 10^7\)
- \(bottomLeft[i][0] \lt topRight[i][0]\)
- \(bottomLeft[i][1] \lt topRight[i][1]\)
Sample Input 1
3
1 1 3 3
2 2 4 4
1 2 3 4Sample Output 1
1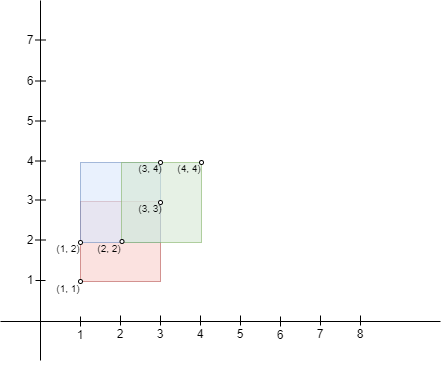
Một hình vuông có cạnh dài \(1\) có thể vừa với vùng giao nhau của hình chữ nhật \(0\) và hình chữ nhật \(1\), vùng giao nhau của hình chữ nhật \(1\) và hình chữ nhật \(2\) hoặc vùng giao nhau của cả \(3\) hình chữ nhật. Do đó diện tích lớn nhất là \(side \times side\) là \(1 \times 1 == 1\). Có thể chứng minh rằng một hình vuông có chiều dài cạnh lớn hơn không thể vừa với bất kỳ vùng giao nhau nào. Lưu ý rằng vùng có thể được hình thành bằng giao điểm của nhiều hơn \(2\) hình chữ nhật.
Sample Input 2
3
1 1 3 3
2 2 4 4
3 1 6 6Sample Output 2
1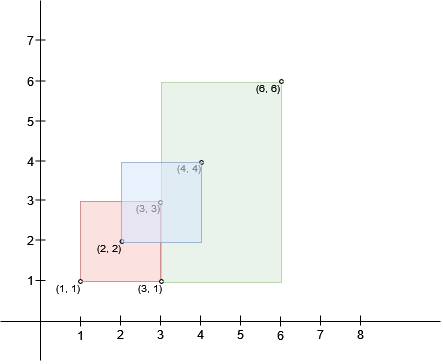
Nhận xét