Có \(n\) điểm tập trung dân cư đông đúc. Các điểm này được đánh số từ \(1\) đến \(n\) \((1 \le n \le 10^4 )\). Mạng lưới giao thông công cộng là \(m\) đường xe lửa cao tốc một ray, mỗi đường nối một cặp điểm dân cư và chạy hai chiều \((0 \le m \le 10^5 )\), và mọi cặp điểm đều có thể đi đến được với nhau. Để tránh sự va chạm giữa các con tàu cao tốc khi chúng có thể đi ngược chiều trên cùng một đường, chính quyền thành phố quyết định sửa lại các con đường đó thành một chiều. Tuy nhiên, sau khi thay đổi thì lại có một vấn đề bất cập xảy ra, đó là: tồn tại các cặp điểm tập trung dân cư không thể đi đến được nhau. Chính vì vậy, chính quyền lại thêm một quyết định nữa, đó là sẽ xây dựng thêm một số ít nhất các tuyến đường mới để đảm bảo từ một điểm bất kỳ có thể đi tới điểm bất kỳ khác bằng tàu cao tốc.

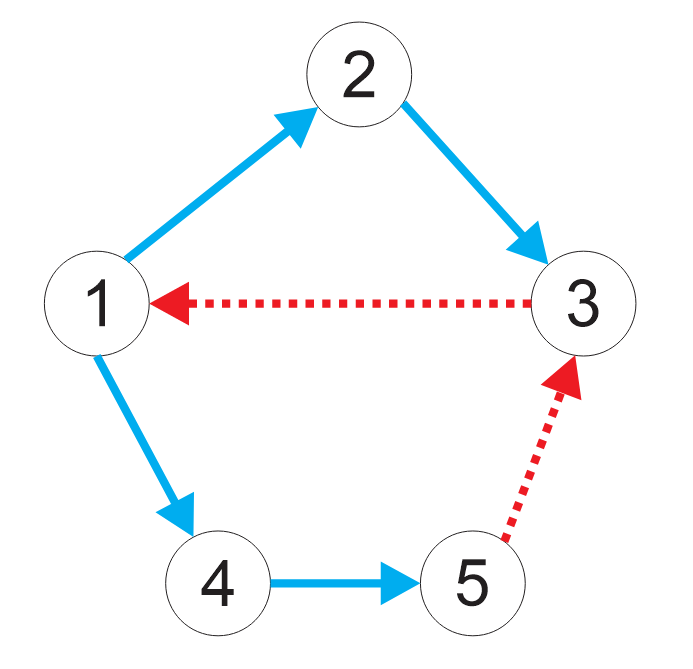
Ví dụ, với \(n = 5\) và hiện có \(4\) đường: \(1 \rightarrow 2, 2 \rightarrow 3, 1 \rightarrow 4\) và \(4 \rightarrow 5\). Để đảm bảo yêu cầu đã nêu, người ta cần xây dựng ít nhất \(2\) đường mới, chẳng hạn \(5 \rightarrow 3\) và \(3 \rightarrow 1\).

Yêu cầu

• Cho \(n, m\) và các cặp \((a, b)\) mô tả mạng giao thông sau khi đã sửa thành đường \(1\) chiều. Mỗi cặp \((a, b)\) xác định tồn tại đường tàu \(a \rightarrow b\). Hãy xác định số lượng tối thiểu các đường cần xây dựng thêm.

Dữ liệu vào

• Dòng đầu tiên chứa \(2\) số nguyên \(n\) và \(m\)
• Mỗi dòng trong \(m\) dòng tiếp theo chứa \(2\) số nguyên \(a\) và \(b\)

Dữ liệu ra

• Số đường mới

Input 1

5 4
1 2
2 3
1 4
4 5

Output 1

2