Một đồ thị liên thông không có chu trình được gọi là cây. Khoảng cách giữa hai đỉnh của cây được định nghĩa là độ dài (tính theo số cạnh) của đường đi ngắn nhất giữa hai đỉnh đó.

Cho một cây gồm \(n\) đỉnh và một số nguyên dương \(k\). Hãy tính số cặp đỉnh khác nhau của cây sao cho khoảng cách giữa chúng bằng \(k\).

Lưu ý rằng cặp \((v, u)\) và \((u, v)\) được coi là một cặp duy nhất.

Dữ liệu vào

• Dòng đầu tiên chứa hai số nguyên \(n\) và \(k\) \((1 \le n \le 50000, 1 \le k \le 500)\) - số đỉnh của cây và khoảng cách yêu cầu giữa các đỉnh.
• \(n - 1\) dòng tiếp theo, mỗi dòng gồm hai số nguyên \(a_i\) và \(b_i\) \((1 \le a_i, b_i \le n, a_i \ne b_i)\), biểu diễn cạnh nối hai đỉnh \(a_i\) và \(b_i\). Tất cả các cạnh đều phân biệt.

Dữ liệu ra

In ra một số nguyên duy nhất — số cặp đỉnh của cây có khoảng cách bằng \(k\).

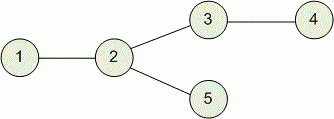
Input 1

5 2
1 2
2 3
3 4
2 5

Output 1

4