Đường Tăng cùng các đồ đệ đang trên đường đi Tây Thiên thỉnh kinh. Họ biết rằng lộ trình của họ là sẽ phải đi qua một ngọn núi có duy nhất một thung lũng.

Bốn thầy trò có một mảng \(a[0...n-1]\) có \(n\) phần tử. Mảng này được gọi là thung lũng nếu có xuất hiện duy nhất một mảng con \(a[l...r]\) thỏa mãn các điều kiện sau:

• \(0 \le l \le r \le n-1,\)
• \(a_l = a_{l+1} = a_{l+2} = ... = a_r,\)
• \(l = 0\) hoặc \(a_{l-1} \gt a_l,\)
• \(r = n-1\) hoặc \(a_r \lt a_{r+1}.\)

Đây là 3 ví dụ mẫu:

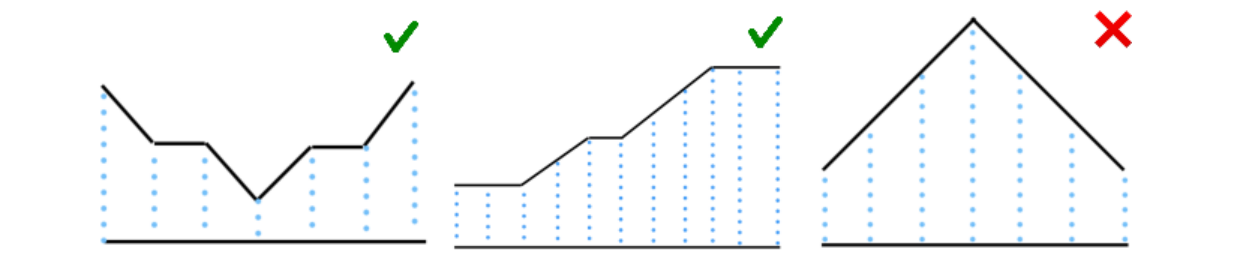
Hình đầu tiên cho ta mảng \([3,2,2,1,2,2,3]\), nó là một thung lũng bởi vì chỉ có mảng con với \(l = r = 3\) thỏa mãn điều kiện.

Hình thứ hai cho ta mảng \([1,1,1,2,3,3,4,5,6,6,6]\), nó là một thung lũng bởi vì chỉ có mảng con với \(l = 0, r = 2\) thỏa mãn điều kiện.

Hình thứ ba cho ta mảng \([1,2,3,4,3,2,1]\) , nó không phải là một thung lũng bởi vì có hai mảng con thỏa mãn điều kiện là \(l = r = 0\) và \(l = r = 6\).

Hãy giúp thầy trò đường tăng xác định xem đây có phải là thung lũng ở ngọn núi trong lộ trình của họ không.

Chú ý: Mảng có vị trí bắt đầu là \(0\).

Dữ liệu vào:

• Dòng đầu chứa 1 số nguyên \(t\) là số lượng test cases \((1 \le t \le 10^4).\).
• Dòng đầu của mỗi test case là một số nguyên \(n (1 \le n \le 2*10^5).\)
• Dòng thứ hai của môi test case là \(n\) số nguyên \(a_i\) \((1 \le a_i \le 10^9).\)

Dữ liệu ra:

• Mỗi test case in ra YES nếu mảng là một thung lũng, in ra NO nếu không phải.

Input:

6
7
3 2 2 1 2 2 3
11
1 1 1 2 3 3 4 5 6 6 6
7
1 2 3 4 3 2 1
7
9 7 4 6 9 9 10
1
1000000000
8
9 4 4 5 9 4 9 10

Output:

YES
YES
NO
YES
YES
NO