Một công ty du lịch muốn tổ chức một chuyến đi qua các địa điểm. Các địa điểm có thể được mô hình hóa bằng một đồ thị liên thông, trong đó mỗi đỉnh là một địa điểm, và mỗi cạnh biểu diễn một con đường hai chiều kết nối giữa hai địa điểm đó. Nhưng không phải con đường đi nào cũng tốt do tình trạng tắc nghẽn giao thông. Các công ty du lịch không muốn các khách hàng thất vọng khi đi qua những con đường không tốt, do đó họ muốn tính toán con đường đi tốt nhất để đi qua các địa điểm. Họ gán cho mỗi con đường một giá trị là số nguyên thỏa mãn, con đường nào tốt hơn sẽ có giá trị cao hơn. Hình trên minh họa \(4\) địa điểm du lịch và \(4\) con đường. Mỗi cạnh trong đồ thị sẽ được gán một giá trị biểu thị chất lượng của con đường đi giữa hai địa điểm. Ví dụ, cạnh \((1,2)\), biểu thị con đường kết nối địa điểm \(1\) và địa điểm \(2\), có chất lượng là \(10\); trong khi cạnh \((3,4)\) có chất lượng là \(5\). Ta định nghĩa chất lượng trên một chuyến đi du lịch là giá trị nhỏ nhất trong tất cả các con đường dọc theo chuyến đi đó. Ví dụ, chất lượng của chuyến đi 1-2-4 là giá trị nhỏ nhất giữa hai cạnh \((1,2)\) và \((2,4)\), hay \(min(10,20)=10\). Tương tự, chất lượng của chuyến đi 1-2-4-3 là giá trị nhỏ nhất của ba cạnh \((1,2)\), \((2,4)\) và \((3,4)\), hay \(min(10,20,5)=5\).

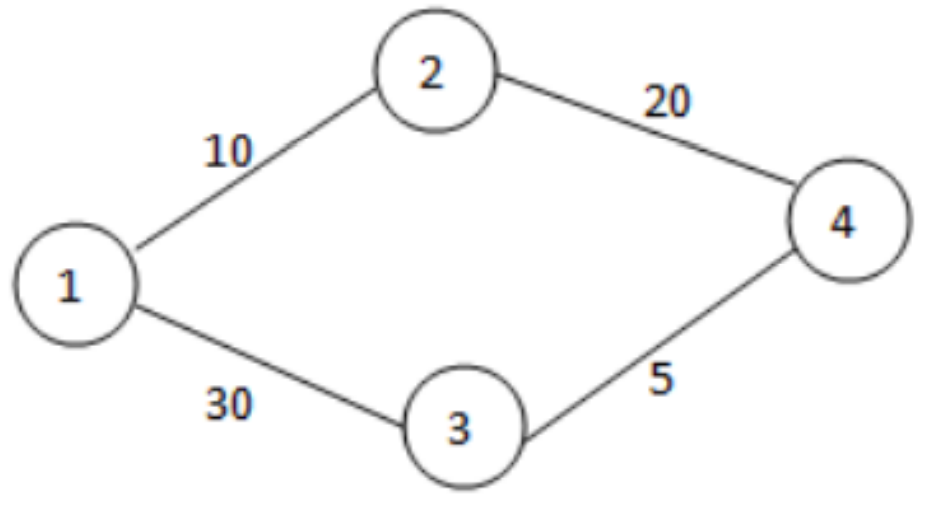
Đỉnh \(1\) là khách sạn nơi các khách du lịch ở. Gọi \(X\) là địa điểm đến của khách du lịch. Công ty du lịch muốn tìm chất lượng cao nhất giữa tất cả các chuyến đi có thể từ đỉnh \(1\) đến đỉnh \(X\). Ví dụ, giả sử bạn muốn thăm đỉnh \(4\), trong số các tuyến đường từ đỉnh 1 đến đỉnh \(4\), tuyến đường đi có chất lượng cao nhất là 1-2-4, và chất lượng là \(10\). Nếu bạn muốn thăm đỉnh \(3\), chất lượng cao nhất của tuyến đường là \(30\).

Công ty du lịch có danh sách \(q\) địa điểm

Yêu cầu của bài toán là ta muốn biết chất lượng cao nhất của tuyến đường từ địa điểm \(1\) tới địa điểm \(X_i (1 \le i \le q)\)

Dữ liệu vào:

• Dòng đầu tiên gồm \(3\) số nguyên \(v, e, q\) biểu thị số lượng các địa điểm, số lượng các con đường và số lượng các điểm đến tương ứng. Các điểm đến được đánh số từ \(1\) tới \(v\), trong đó địa điểm \(1\) là khách sạn bắt đầu chuyến đi.
• \(e\) dòng tiếp theo, mỗi dòng gồm \(3\) số nguyên \(v_1, v_2, w\) trong đó \(v_1, v_2\) biểu thị con đường nối giữa hai địa điểm và \(w\) biểu thị chất lượng của con đường này \((0 \le w \le 100000)\).
• \(q\) dòng tiếp theo mỗi dòng gồm một số nguyên \(x\) biểu thị một điểm đến trong tuyến đường du lịch và \(x \neq 1\) (tức là khách sạn không phải điểm đến).

Dữ liệu ra:

• Với mỗi điểm đến, đưa ra một số nguyên biểu thị chất lượng lớn nhất của tuyến đường từ địa điểm \(1\) đến nó.

Input 1

4 4 2
1 2 10
1 3 30
2 4 20
3 4 5
3
4

Output 1

30
10

Chú ý:

• 20% số điểm ứng với đồ thị có một chu trình, hay mỗi đỉnh có bậc là hai, với điều kiện \(V \le 100; E \le 100; Q \le 50\)
• 20% số điểm ứng với đồ thị liên thông tổng quát, với điều kiện \(V \le 500; E \le 4000; Q \le 100\).
• 20% số điểm ứng với đồ thị liên thông quát, với điều kiện \(V \le 50000; E \le 100000; Q \le 10000\)
• 40% số điểm ứng với đồ thị liên thông tổng quát, với điều kiện \(V \le 500000; E \le 5000000; Q \le V - 1\)