Cho bảng gồm \(n\) hàng và \(m\) cột. Mỗi ô của bảng được gán một số nguyên. Ta quy ước một hình chữ L là tập hợp các ô vuông con của bảng như hình vẽ (hoặc là ảnh của hình vẽ qua phép quay \(\pm90^\circ\), \(\pm180^\circ\)).

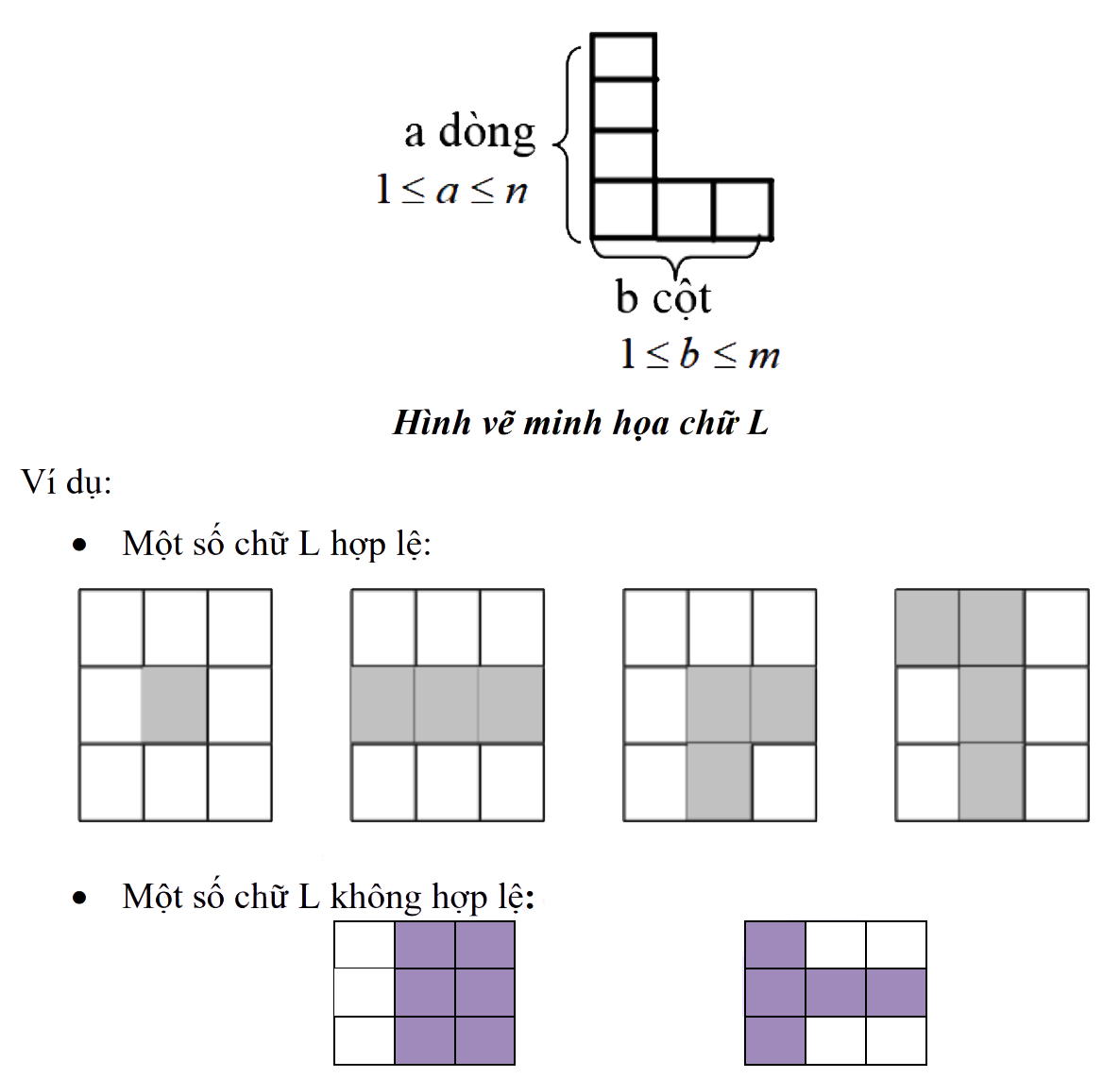
Yêu cầu:

• Tìm tổng lớn nhất của các ô tạo thành chữ L.

Dữ liệu vào:

• Dòng đầu tiên gồm hai số nguyên \(n\) và \(m\), trong đó \(n\) và \(m\) là số hàng và số cột của bảng (\(1 \leq n, m \leq 1000\)).
• \(n\) dòng tiếp theo, mỗi dòng gồm \(m\) số nguyên \(a_{ij}\) (\(1 \leq i \leq n, 1 \leq j \leq m, -10^9 \leq a_{ij} \leq 10^9\)), biểu thị giá trị trong các ô của bảng.

Dữ liệu ra:

• Ghi một số nguyên là tổng lớn nhất của các ô tạo thành chữ L.

Input 1

2 2
8 1
3 4

Output 1

15

Giải thích

• Có thể chọn các số tạo thành chữ L: \(8, 3, 4\)

Chú ý:

• 10% số điểm ứng với \(1 \leq n, m \leq 2\)
• 10% số điểm ứng với \(n = 1\)
• 30% số điểm ứng với \(1 \leq n, m \leq 300\)
• 20% số điểm ứng với \(0 \leq a_{ij} \leq 10^9\) với \(1 \leq i \leq n, 1 \leq j \leq m\)
• 30% số điểm còn lại không có giới hạn gì thêm.