Có \(n\) đường thẳng đứng được vẽ sao cho hai điểm đầu của đường thẳng thứ i là (i, 0) và (i, chiều cao[i]).

Tìm hai đường thẳng cùng với trục x tạo thành một thùng chứa sao cho thùng chứa nhiều nước nhất.

Tính lượng nước tối đa mà thùng chứa có thể chứa được.

Ví dụ:

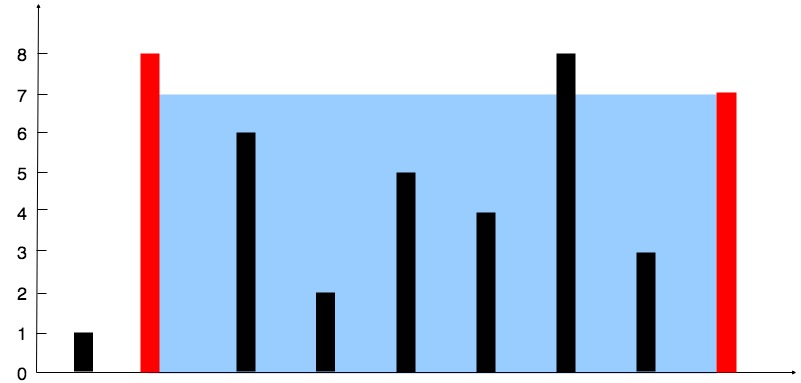
Input:

9
1 8 6 2 5 4 8 3 7

Output:

49

Input

• Dòng đầu tiên là số lượng đường thẳng \(n\)
• Dòng tiếp theo chứa \(n\) số nguyên

Output

• Tính lượng nước tối đa mà thùng chứa có thể chứa được.

Ràng buộc:

• \(n == height.length\)
• \(2 \le n \le 10^5\)
• \(0 \le height[i] \le 10^4\)