Hình chữ nhật bốn màu
Xem dưới dạng PDFTrên mặt phẳng tọa độ Đề các vuông góc \(Oxy\) cho \(n\) điểm phân biệt \(A_i(x_i,y_i) i=1,2,3...,n\). Mỗi điểm \(A_i\) được tô bởi màu \(C_i\) thuộc \({1,2,3,4}\). Ta gọi hình chữ nhật bốn màu là hình chữ nhật thỏa mãn hai điều kiện sau:
- Bốn đỉnh của hình chữ nhật là bốn điểm trong \(n\) điểm đã cho và được tô bởi bốn màu khác nhau.
- Các cạnh của hình chữ nhật song song với một trong hai trục tọa độ.
Yêu cầu: Cho biết tọa độ và màu của \(n\) điểm, hãy đếm số lượng hình chữ nhật bốn màu.
Input
- Dòng đầu tiên chứa số nguyên dương \(n\) \((4 \le n \le 10^5)\) là số lượng điểm trên mặt phẳng.
- Dòng thứ \(i\) trong \(n\) dòng tiếp theo chứa ba số nguyên \(x_i,y_i,c_i (|x_i|, |y_i| \le 200)\) là thông tin về tọa độ và màu của điểm thứ \(i (i=1,2,3...n)\)
- Các số trên cùng một dòng được ghi cách nhau ít nhất một dấu cách.
Output
Ghi ra trên một dòng số lượng hình chữ nhật đếm được. .
Giới hạn:
- 50% số test ứng với 50% số điểm của bài có \(n \le 100\)
Input
7
0 0 1
0 2 4
2 2 2
2 -1 3
0 -1 1
-1 -1 4
-1 2 1Output
2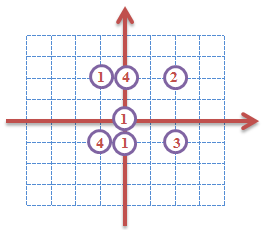
Nhận xét