Có một cái la bàn chỉ thẳng về phía sao mai. Nó chỉ có thể chỉ về một trong 8 hướng : 4 hướng chính (Đông,Tây,Nam,Bắc) hoặc 4 hướng phụ (Đông Bắc, Đông Nam, Tây Bắc, Tây Nam). Còn không nó sẽ bị vỡ.

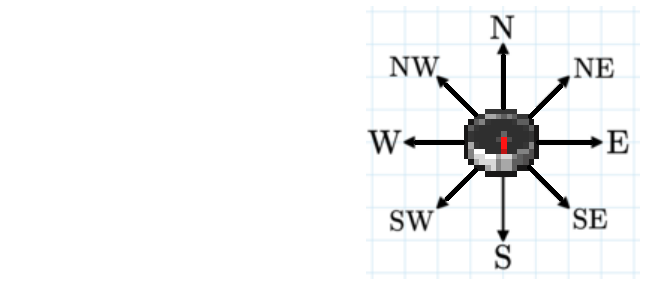
Cho \(n\) điểm phân biệt có tọa độ nguyên trên 1 mặt phẳng. Hỏi có bao nhiêu cách bạn có thể đặt la bàn ở 1 điểm và sao mai ở một điểm để la bàn không bị vỡ ?

Giá trị vào:

• Dòng đầu là một số nguyên \(t\) là số lượng test cases \((1 \le t \le 10^3).\)
• Dòng đầu của mỗi test case chứa 1 số nguyên \(n\) là số điểm trên mặt phẳng \((2 \le n \le 10^3).\)
• \(n\) dòng tiếp theo mỗi dòng chứa 2 số nguyên \(x_i,y_i\) là tọa độ của mỗi điểm trên mặt phẳng \((-10^9 \le x_i,yi \le 10^9).\)

Giá trị ra:

• Mỗi test case in ra 1 số nguyên là số lượng của mỗi cặp điểm mà không làm cho la bàn bị vỡ.

Input:

5
3
0 0
-1 -1
1 1
4
4 5
5 7
6 9
10 13
3
-1000000000 1000000000
0 0
1000000000 -1000000000
5
0 0
2 2
-1 5
-1 10
2 11
3
0 0
-1 2
1 -2

Output:

6
2
6
8
0

Giải thích:

Ở test case đầu tiên, bất cứ cặp điểm nào trên trục tọa độ nào cũng không làm cho la bàn bị vỡ:

• La bàn ở tọa độ \((0,0)\), sao mai ở tọa độ \((-1,-1)\): la bàn sẽ chỉ về hướng Tây Nam.
• La bàn ở tọa độ \((0,0)\), sao mai ở tọa độ \((1,1)\): la bàn sẽ chỉ về hướng Đông Bắc.
• La bàn ở tọa độ \((-1,-1)\), sao mai ở tọa độ \((0,0)\): la bàn sẽ chỉ về hướng Đông Bắc.
• La bàn ở tọa độ \((-1,-1)\), sao mai ở tọa độ \((1,1)\): la bàn sẽ chỉ về hướng Đông Bắc.
• La bàn ở tọa độ \((1,1)\), sao mai ở tọa độ \((0,0)\): la bàn sẽ chỉ về hướng Tây Nam.
• La bàn ở tọa độ \((1,1)\), sao mai ở tọa độ \((-1,-1)\): la bàn sẽ chỉ về hướng Tây Nam.

Ở test case thứ hai, chỉ có hai cặp điểm không làm cho la bàn bị vỡ.

• La bàn ở tọa độ \((6,9)\), sao mai ở tọa độ \((10,13)\): la bàn sẽ chỉ về hướng Đông Bắc.
• La bàn ở tọa độ \((10,13)\), sao mai ở tọa độ \((6,9)\): la bàn sẽ chỉ về hướng Tây Nam.