Trong mặt phẳng, cho \(n\) đường thẳng. Các đường thẳng này có thể cắt nhau tại các giao điểm.

Như chúng ta đã biết, cứ qua \(2\) điểm ta lại xác định được \(1\) đường thẳng. Hai đường thẳng được gọi là trùng nhau nếu giữa chúng có ít nhất \(2\) điểm chung.

Nhiệm vụ của bạn là xác định xem với n đường thẳng cắt nhau trên mặt phẳng (các đường thẳng có thể được vẽ tùy ý), thì qua các giao điểm của chúng, ta có thể xác định được tối đa bao nhiêu đường thẳng phân biệt (không trùng nhau), bao gồm cả các đường thẳng ban đầu.

Ví dụ:

Với \(n = 4\), kết quả sẽ là \(numberOfLine(4) = 7\). Với hình minh họa, ta có thể thấy rằng các giao điểm của \(4\) đường thẳng (màu xanh, đỏ, vàng và đen) là \(A, B, C, D, E \) và \(F\). Qua tất cả các giao điểm, ta có thể xác định được rằng có \(7\) đường thẳng đi qua các giao điểm đó. Bao gồm: \(AE, AC, EB, FC, FB, EC\) và \(AD\).

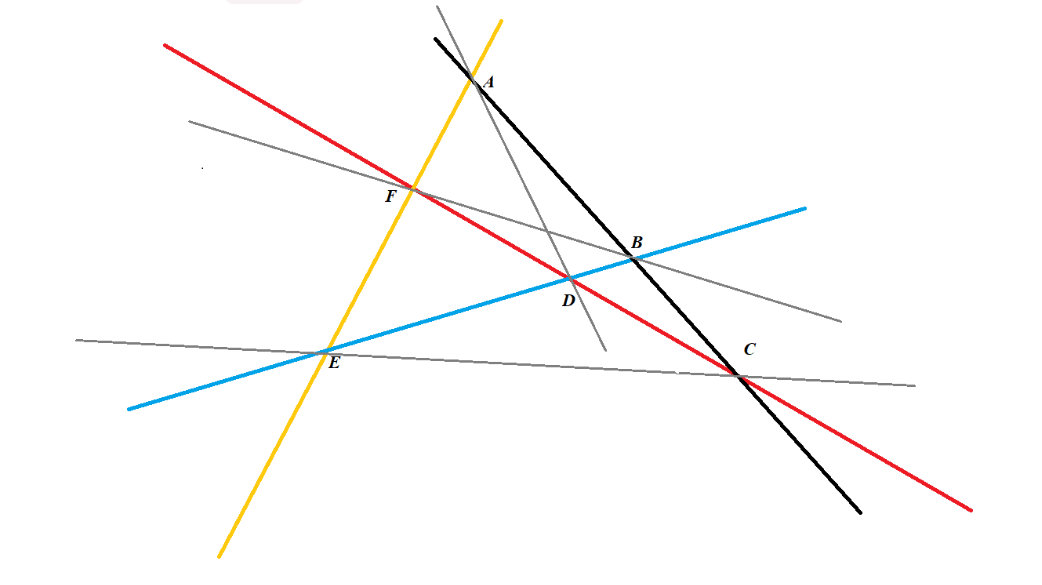
Lưu ý:

• Đường thẳng đi qua \(A, E\) và đường thẳng đi qua \(A, F\) trùng nhau nên ta chỉ tính một lần. Các trường hợp tương tự cũng chỉ tính một lần.

Dữ liệu vào

• Một số nguyên \(n\) \((0 \lt n \le 10000)\)

Dữ liệu ra

• Một số biểu thị số đường thẳng phân biệt lớn nhất được xác định bởi các giao điểm của \(n\) đường thẳng trên mặt phẳng.

Input 1

3

Output 1

3

Input 2

4

Output 2

7

Input 3

5

Output 3

20

Input 4

13

Output 4

2158