Cho một tứ diện, đánh dấu các đỉnh lần lượt là \(A, B, C, D\).

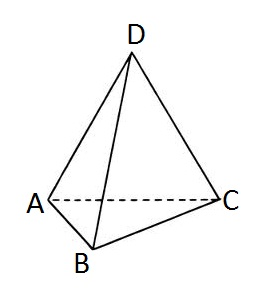
Một con kiến đang đứng trên đỉnh \(D\) của tứ diện. Con kiến khá tích cực di chuyển và nó không chịu nhàn rỗi. Với mỗi bước đi, nó bước từ một đỉnh tới đỉnh khác dọc theo một số cạnh của tứ diện. Con kiến không bao giờ chịu đứng yên ở một chỗ.

Yêu cầu

• Đếm số cách mà con kiến có thể đi từ đỉnh \(D\) ban đầu rồi quay về chính nó trong đúng \(n\) bước. Nói cách khác, bạn sẽ được yêu cầu tìm ra số con đường tuần hoàn khác nhau có chiều dài \(n\) từ đỉnh \(D\) đến chính nó. Vì số có thể khá lớn nên bạn nên in theo modulo \((10^9 + 7)\).

Dữ liệu đầu vào:

• Dòng đầu tiên chứa số nguyên duy nhất \(n\) \((1 \le n \le 10^{18})\) - chiều dài của đường đi.

Dữ liệu đầu ra:

• In số nguyên duy nhất là kết quả tìm được modulo \((10^9+ 7)\).

Input 1

2

Output 1

3

Giải thích

Có \(3\) cách đi có thể với bộ dữ liệu trên là là:

• \(D - A - D\)
• \(D - B - D\)
• \(D - C - D\)

Input 2

4

Output 2

21