Bạn được cho một cây gồm \(n\) đỉnh. Cây là đồ thị vô hướng, liên thông, không chu trình, có \(n - 1\) cạnh. Mỗi đỉnh \(v\) được gán màu: \(a_v = 1\) nếu đỉnh \(v\) màu trắng, và \(0\) nếu đỉnh \(v\) màu đen.

Yêu cầu

• Đối với mỗi đỉnh \(v\), hãy tìm sự chênh lệch lớn nhất giữa số đỉnh trắng và đỉnh đen trong một cây con bất kỳ (liên thông) có chứa đỉnh \(v\).

Nói cách khác: với mỗi đỉnh \(v\), tìm một cây con (tức là tiểu đồ thị liên thông của cây gốc) có chứa \(v\), sao cho giá trị \(cnt_w - cnt_b\) lớn nhất, với:

• \(cnt_w\): số đỉnh trắng trong cây con
• \(cnt_b\): số đỉnh đen trong cây con

Dữ liệu vào

• Dòng đầu: Số nguyên \(n\) \((2 \le n \le 2 \times 10^5)\) - số đỉnh của cây.
• Dòng hai: \(n\) số nguyên \(a_1, a_2, ..., a_n\) \((0 \le a_i \le 1)\), trong đó \(a_i\) là màu của đỉnh \(i\).
• Sau đó là \(n - 1\) dòng, mỗi dòng hai số nguyên \(u_i, v_i\) \((1 \le u_i, v_i \le n, u_i \neq v_i)\) cho biết có cạnh nối hai đỉnh đó.

Dữ liệu ra

• In ra \(n\) số nguyên \(res_1, res_2, ..., res_n\), trong đó \(res_i\) là sự chênh lệch lớn nhất giữa số trắng và đen trong một cây con có chứa đỉnh \(i\).

Input 1

9
0 1 1 1 0 0 0 0 1
1 2
1 3
3 4
3 5
2 6
4 7
6 8
5 9

Output 1

2 2 2 2 2 1 1 0 2

Input 2

4
0 0 1 0
1 2
1 3
1 4

Output 2

0 -1 1 -1

Ghi chú

• Trong ví dụ đầu, các đỉnh màu đen được viền đậm.

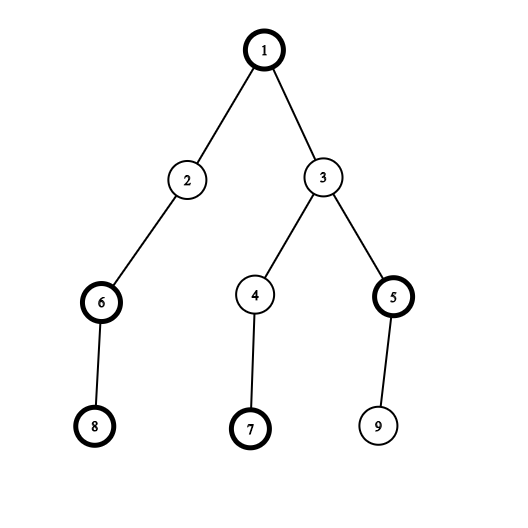
• Trong ví dụ thứ hai, cây con tốt nhất cho đỉnh 1 là phần gồc bao gồm đỉnh 1 và 3. Còn lại các đỉnh tự thân là cây con tối ưu nhất của chính nó.