Bạn được cho một cây (đồ thị vô hướng liên thông không có chu trình) gồm \(n\) đỉnh. Bạn sẽ chơi một trò chơi trên cây này.

Ban đầu tất cả các đỉnh đều màu trắng. Ở lượt đầu tiên, bạn chọn một đỉnh và sơn nó thành màu đen. Sau đó, ở mỗi lượt, bạn chọn một đỉnh trắng kề (nối bởi một cạnh) với bất kỳ đỉnh đen nào và sơn nó thành màu đen.

Mỗi lần khi bạn chọn một đỉnh (kể cả lượt đầu), bạn nhận được số điểm bằng kích thước của thành phần liên thông chỉ gồm các đỉnh trắng chứa đỉnh bạn vừa chọn. Trò chơi kết thúc khi tất cả các đỉnh được sơn thành màu đen.

Hãy xem ví dụ sau:

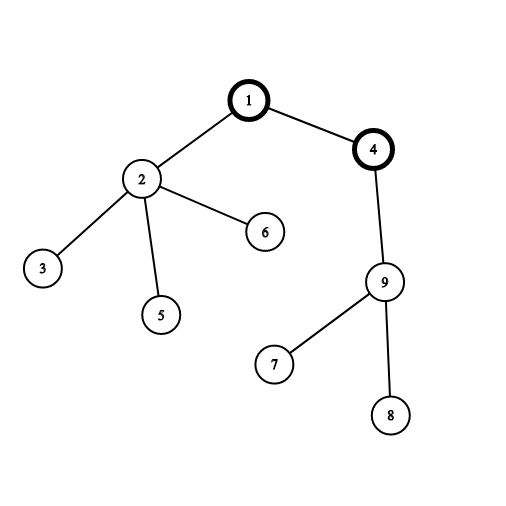
Ví dụ minh họa một cây với 9 đỉnh. Các đỉnh 1 và 4 đã được sơn đen. Nếu bạn chọn đỉnh 2, bạn sẽ nhận được 4 điểm ứng với thành phần liên thông gồm các đỉnh 2, 3, 5 và 6. Nếu bạn chọn đỉnh 9, bạn sẽ nhận được 3 điểm ứng với thành phần liên thông gồm các đỉnh 7, 8 và 9.

Nhiệm vụ của bạn là tối đa hóa số điểm bạn nhận được.

Dữ liệu vào

• Dòng đầu tiên chứa số nguyên n - số đỉnh trong cây \((2 \le n \le 2·10^5)\).
• Mỗi trong n-1 dòng tiếp theo mô tả một cạnh của cây. Dòng i gồm hai số nguyên ui và vi — chỉ số hai đỉnh mà cạnh đó nối \((1 \le u_i, v_i \le n, u_i ≠ v_i)\).
• Đảm bảo rằng các cạnh cho trước tạo thành một cây.

Dữ liệu ra

• In ra một số nguyên - số điểm tối đa bạn có thể nhận được nếu chơi một cách tối ưu.

Input 1

9
1 2
2 3
2 5
2 6
1 4
4 9
9 7
9 8

Output 1

36

Input 2

5
1 2
1 3
2 4
2 5

Output 2

14