Bạn được cho một cây gồm chính xác \(n\) đỉnh. Cây là một đồ thị vô hướng, liên thông và không chu trình, có \(n-1\) cạnh. Mỗi đỉnh \(v\) được gán một giá trị \(a_v\).

Gọi \(dist(x, y)\) là khoảng cách giữa hai đỉnh \(x\) và \(y\), tính bằng số cạnh trên đường đi ngắn nhất.

Chúng ta định nghĩa chi phí của cây theo cách sau:

• Chọn một đỉnh \(v\) làm gốc.
• Khi đó, chi phí là: \(\sum\limits_{i = 1}^{n} dist(i, v) \cdot a_i\)

Nhiệm vụ của bạn là tính giá trị chi phí lớn nhất có thể nhận được khi bạn được chọn vị trí gốc \(v\) tự do.

Dữ liệu vào

• Dòng đầu: Số nguyên \(n\) \((1 \le n \le 2 \times 10^5)\) - số đỉnh trong cây.
• Dòng tiếp theo: \(n\) số nguyên \(a_1, a_2, ..., a_n\) \((1 \le a_i \le 2 \times 10^5)\), trong đó \(a_i\) là giá trị đỉnh \(i\).
• Sau đó là \(n-1\) dòng, mỗi dòng hai số nguyên \(u_i\), \(v_i\) \((1 \le u_i, v_i \le n, u_i \neq v_i)\) cho biết có cạnh nối hai đỉnh \(u\) và \(v\).

Bảo đảm các cạnh cho trước tạo thành một cây hợp lệ.

Dữ liệu ra

• In ra một số nguyên duy nhất - chi phí lớn nhất có thể của cây khi chọn vị trí gốc tự do.

Input 1

8
9 4 1 7 10 1 6 5
1 2
2 3
1 4
1 5
5 6
5 7
5 8

Output 1

121

Input 2

1
1337

Output 2

0

Ghi chú

Ví dụ 1: chọn đỉnh 3 làm gốc:

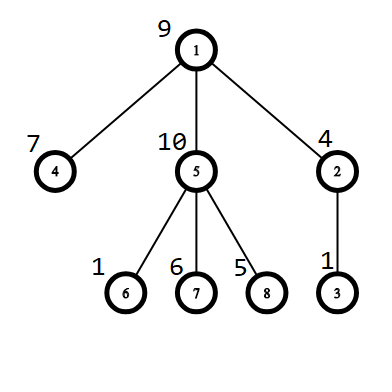
• dist(1,3) * a_1 = 2 * 9 = 18
• dist(2,3) * a_2 = 1 * 4 = 4
• dist(3,3) * a_3 = 0 * 1 = 0
• dist(4,3) * a_4 = 3 * 7 = 21
• dist(5,3) * a_5 = 3 * 10 = 30
• dist(6,3) * a_6 = 4 * 1 = 4
• dist(7,3) * a_7 = 4 * 6 = 24
• dist(8,3) * a_8 = 4 * 5 = 20 => Tổng = 121

Ví dụ 2: cây chỉ có một đỉnh thì chi phí luôn bằng 0.