Bài 1. Paradoks
Xem dưới dạng PDFVào một buổi tối trăng tròn, khi đồng hồ điểm nửa đêm, năm người bạn thấy mình sẵn sàng chơi một trò chơi bí ẩn như chính đêm nay. Họ ngồi thành vòng tròn, theo chiều kim đồng hồ: Igor, Lea, Marino, Sonja và Viktor. Trò chơi gồm \(N\) vòng. Vòng đầu tiên được bắt đầu bởi Sonja, và mỗi vòng tiếp theo được bắt đầu bởi người thắng của vòng trước. Mỗi người chơi giữ \(N\) lá bài trong tay. Tất cả các lá bài đều không màu và có một số tự nhiên từ \(1\) đến \(9\) trên đó. Khi một người chơi ra bài, họ chọn màu cho lá bài đó. Họ có thể chọn một trong bốn màu (đỏ, xanh dương, vàng, xanh lá) với điều kiện là lá bài như vậy (kết hợp của số và màu đó) chưa được chơi trong trò chơi. Trong phần còn lại của văn bản, thuật ngữ chơi lá bài xanh dương, ví dụ, đề cập đến quy trình chơi lá bài và tuyên bố nó là màu xanh dương. Trong mỗi vòng, các người chơi, theo chiều kim đồng hồ, mỗi người chơi một lá bài cho đến khi lượt quay lại người đã bắt đầu vòng, tức là cho đến khi mỗi người chơi đã chơi một lá bài. Lá bài đầu tiên được chơi trong một vòng xác định cái gọi là màu vòng, và tất cả người chơi tiếp theo được yêu cầu chơi bài có màu đó. Nếu bất kỳ người chơi nào không chơi được lá bài có màu của vòng hiện tại, người ta giả định rằng người chơi không còn lá bài màu đó trong tay - và họ bị cấm chơi lá bài màu đó trong phần còn lại của trò chơi.
Người thắng của mỗi vòng là:
- Người chơi lá bài đỏ có số cao nhất.
- Nếu không có lá bài đỏ nào được chơi, người chơi số cao nhất của màu vòng.
Đôi khi, người chơi thực hiện một nước đi mà họ không nên: hoặc họ chơi một lá bài đã được chơi hoặc chơi một lá bài có màu mà họ trước đó đã tuyên bố không còn. Nước chơi này được gọi là paradoks. Khi một paradoks xảy ra, nước chơi hoàn toàn bị bỏ qua trong việc tính toán người thắng vòng và phần còn lại của trò chơi. Ví dụ, nếu một lá bài được chơi lần đầu tiên như một paradoks, trong phần còn lại của trò chơi, nó được coi như chưa được chơi. Đảm bảo rằng người chơi đầu tiên trong một vòng sẽ không bao giờ chơi một paradoks trong vòng đó.
Các anh hùng của chúng ta đã không gặp nhau trong một thời gian dài và không chú ý kỹ đến trò chơi, vì vậy họ yêu cầu sự giúp đỡ của bạn. Viết một chương trình, cho các lá bài được chơi theo thứ tự từng vòng, in ra bao nhiêu paradoks đã xảy ra và liệt kê chúng theo thứ tự chúng xảy ra. Đối với mỗi paradoks, in vòng mà nó xảy ra và người chơi đã gây ra nó.
Dữ liệu vào
- Dòng đầu tiên của input chứa một số tự nhiên \(N\) \((1 \le N \le 10)\), số vòng.
- Trong \(N\) dòng tiếp theo của input, có \(5\) từ, mỗi từ dài \(2\) ký tự, đại diện cho các lá bài được chơi trong vòng đó, theo thứ tự chúng được chơi. (Chú ý: người chơi đầu tiên trong mỗi vòng không nhất thiết phải giống nhau.)
- Ký tự đầu tiên của mỗi từ đại diện cho màu của lá bài mà người chơi đã chơi và sẽ là một trong các chữ cái sau: 'C' - đỏ, 'P' - xanh dương, 'Y' - vàng, 'Z' - xanh lá. Ký tự thứ hai của mỗi từ sẽ là một số tự nhiên từ \(1\) đến \(9\) (bao gồm), đại diện cho số trên lá bài.
Ví dụ, từ 'Y5' sẽ đại diện cho một lá bài vàng có số \(5\).
Dữ liệu ra
- In một số duy nhất \(a\), số lượng paradoks đã xảy ra.
- Trong a dòng tiếp theo, cho mỗi paradoks trong số a paradoks, in số vòng và tên của người chơi đã gây ra nó, bằng chữ in hoa.
- Các paradoks nên được in theo thứ tự chúng xảy ra.
Chấm điểm
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | 10 | Sonja sẽ là người thắng của tất cả các vòng, và tất cả paradoks sẽ xảy ra do lặp lại một lá bài đã được chơi. |
| 2 | 10 | Tất cả paradoks xảy ra sẽ được gây ra bởi việc lặp lại một lá bài đã được chơi. |
| 3 | 30 | Không có ràng buộc bổ sung. |
Input 1
4
Y5 Z3 Y6 C2 Y1
Z4 Z7 Z2 Y2 P3
Z6 Z7 Z1 Y2 C2
P6 P8 P8 Z7 Y9Output 1
6
2 VIKTOR
3 SONJA
3 LEA
4 VIKTOR
4 IGOR
4 LEAInput 2
3
P1 Y9 Z5 Y1 Z5
P5 Y7 Z3 Y8 P1
C6 Y8 P5 Z1 Z8Output 2
4
1 MARINO
2 MARINO
3 VIKTOR
3 IGORInput 3
1
Y4 P9 Y8 Z5 Z3Output 3
0Giải thích ví dụ đầu tiên:
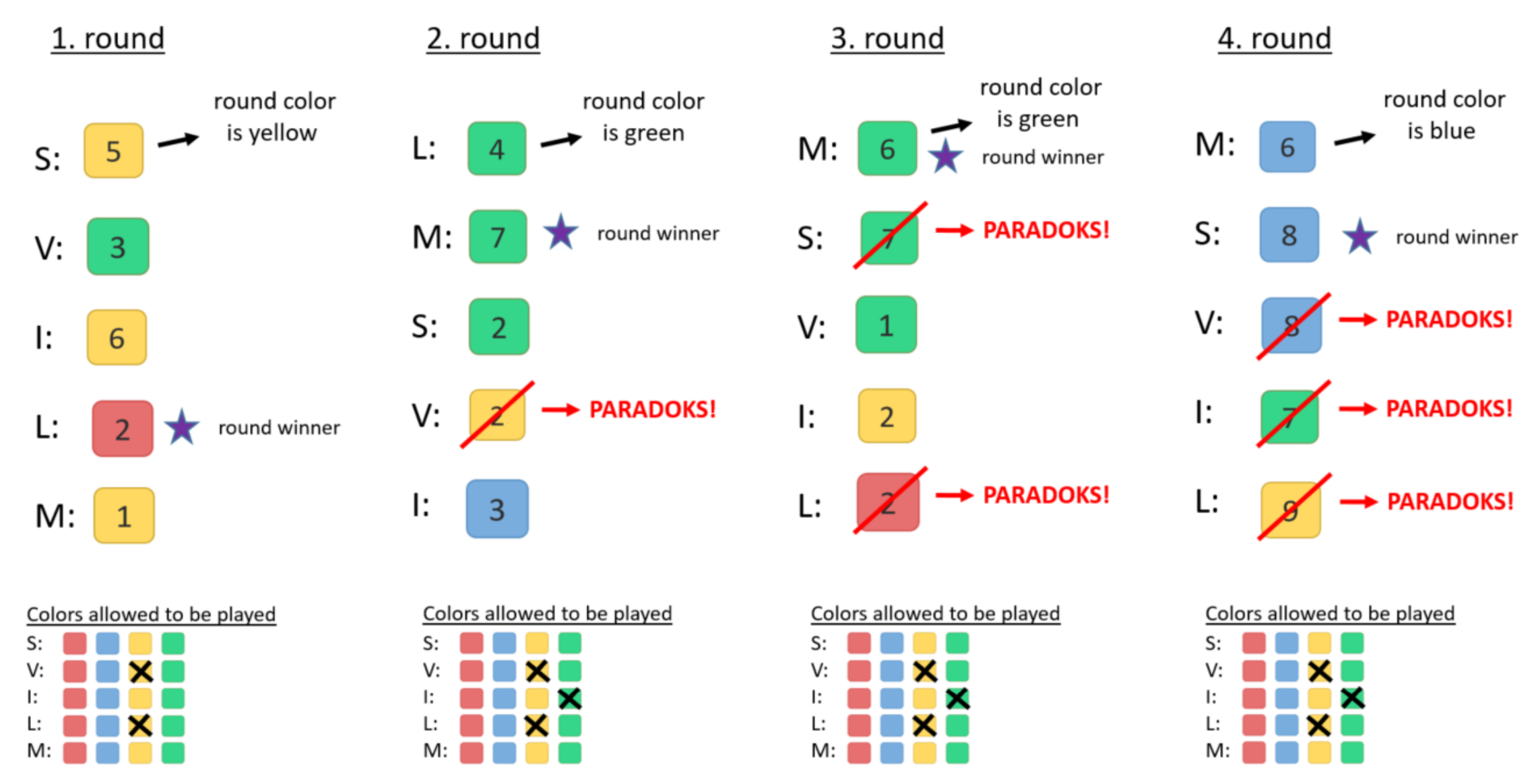
Diễn biến của trò chơi được hiển thị trong hình bên dưới (ở trang tiếp theo). Trong vòng 1, Viktor và Lea không chơi lá bài vàng (màu của vòng), vì vậy người ta giả định rằng họ không còn lá bài vàng trong tay và bị cấm tuyên bố bất kỳ lá bài nào là vàng trong phần còn lại của trò chơi. Đây là lý do cho paradoks của Viktor trong vòng 2 và paradoks của Lea trong vòng cuối. Lưu ý: trong vòng 2, do paradoks, nước đi của Viktor bị bỏ qua, và chúng ta không rút ra thêm kết luận nào. Ngoài ra, lá bài Y2 không được coi là đã chơi, đó là lý do tại sao Igor không nhận được paradoks khi chơi lá bài đó trong vòng 3. Tất cả các paradoks trong vòng 3 và 4 (ngoại trừ cái cuối cùng) xảy ra vì một lá bài được chơi đã được chơi trước đó trong trò chơi.
Nhận xét