Hệ thống thoát nước ngầm hiện đại của Vũng Tàu gồm \(n\) chốt được đánh số từ \(1\) đến \(n\) với \(m\) đường ống hai chiều nối giữa các cặp chốt.

Ban đầu, các chốt trong hệ thống được đóng nắp và nước bên ngoài không thể chảy vào hệ thống. Khi có một chốt \(x\) được mở nắp, dòng nước bên ngoài sẽ chảy đến các chốt khác có đường ống thông với chốt \(x\) giúp giảm bớt ngập cho thành phố.

Nhà quản lý muốn mở nắp của không quá \(k\) \((1 \le k \le n)\) chốt sao cho có thể dẫn nước từ bên ngoài vào và thông qua các đường ống để dẫn nước sang nhiều chốt nhất có thể. Ngoài ra, để giảm chi phí vận hành, các chốt được mở nắp phải có cùng số lượng đường ống nối đến trực tiếp.

Yêu cầu:

• Cho biết dòng nước có thể chảy đến được nhiều nhất là bao nhiêu chốt?

Dữ liệu vào:

• Dòng đầu chứa ba số \(n, m, k\) \((1 \le k \le n \le 100000; 0 \le m \le min (n \times (n - 1) / 2, 100000))\).
• \(m\) dòng tiếp theo, mỗi dòng chứa hai số nguyên \(i, j\) cho biết có đường ống nối trực tiếp giữa chốt \(i\) và \(j\) \((i \neq j; 1 \le i, j \le n)\). Dữ liệu đảm bảo mỗi cặp chốt có nhiều nhất một đường ống nối trực tiếp.

Dữ liệu ra:

• Một số nguyên là số lượng chốt nhiều nhất mà nước có thể chảy đến khi mở nắp không quá \(k\) chốt và đảm bảo các chốt được mở phải có cùng số lượng đường ống nối trực tiếp (có thể cùng bằng \(0\)).

Input 1

7 4 3
1 2
2 3
2 6
4 5

Output 1

6

Giải thích

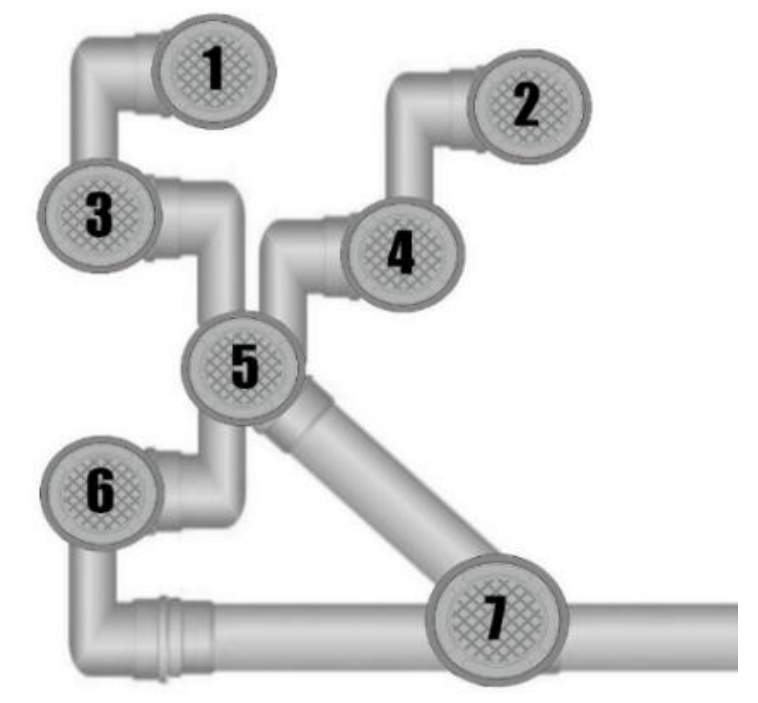
Chọn chốt 1 và chốt 4 (có cùng số đường ống nối trực tiếp là 1). Mở chốt 1, nước chảy đến chốt: 1, 2, 3, 6; mở chốt 4, nước chảy đến chốt: 4, 5.

Input 2

6 0 5

Output 2

5

Giải thích

Cả 6 chốt có cùng số lượng đường ống nối trực tiếp là 0 nên có thể chọn 5 chốt bất kỳ.

Ràng buộc:

• 25% số test có \(k = 1\).
• 25% số test có \(1 \le n \le 100\).
• 50% số test không có ràng buộc gì thêm.