Mô hình giá là một trong những công cụ yếu thích của những nhà đầu tư (NĐT). Bằng việc theo dõi giá giao dịch của một mặt hàng trong một khoảng thời gian, NĐT có thể tìm thấy một mô hình giá được lặp lại trong những thời điểm khác nhau để từ đó có những quyết định đầu tư hợp lý.

Một mô hình giá \(H\) có chiều dài \(N\) được cho bởi một hoán vị \((H_1, H_2, ..., H_N)\) của tập các số \({1, 2, ..., N}\). Các giao dịch này được đánh số thứ tự từ \(1\) đến \(N\), hoán vị trên cho biết trong \(N\) giao dịch liên tiếp thì các mức so sánh giá giao dịch lần lượt là \((H_1, H_2, ..., H_N)\). Mức giá giao dịch thấp nhất là \(1\), tiếp đến là \(2\), ... và mức giá giao dịch cao nhất là \(N\). Khi xét \(N\) giao dịch \(A\) liên tiếp bất kỳ, ta nói mô hình giá \(H\) được lặp lại nếu so sánh giá giao dịch tại phiên thứ \(i\) và \(j\) là \(A_i \lt A_j\) khi và chỉ khi \(H_i \lt H_j\) với mọi \(i, j\) trong khoảng từ \(1\) đến \(N\).

Yêu cầu:

• Cho trước \(M\) phiên giao dịch, các giao dịch này được đánh số từ \(1\) đến \(M\), và một mô hình giá có chiều dài \(N\). Hãy viết một chương trình cho biết mô hình giá trên được lặp bao nhiêu lần và vị trí những lần đó trong \(M\) giao dịch.

Dữ liệu vào

• Dòng đầu là hai số nguyên \(N\) và \(M\) cho biết chiều dài của mô hình giá và số phiên giao dịch đang xét.
• Dòng thứ hai chứa \(N\) số nguyên \(H_i\) là một hoán vị của tập các số \({1, 2, ..., N}\), trong đó \(1 \le Hi \le N\) và \(Hi \neq Hj\) với mọi \(i, j\).
• Dòng thứ ba chứa \(M\) số nguyên Gi \((1 \le Gi \le 10^9)\) lần lượt là giá giao dịch trong \(M\) phiên. Để thuận lợi trong thống kê, bạn có thể giả sử các số Gi luôn khác nhau.

Dữ liệu ra

• Dòng đầu là một số nguyên \(D\) cho biết số lần mô hình giá được lặp lại.
• Dòng thứ hai chứa \(D\) số nguyên là số các phiên giao dịch đầu tiên khi mô hình giá lặp lại, các số chỉ này được sắp xếp tăng dần. Nếu \(D = 0\) thì dòng thứ hai không xuất hiện.

Ràng buộc

• 20% test ứng với 20% số điểm có \(1 \lt N \le 100\) và \(1 \lt M \le 1000\)
• 30% test ứng với 20% số điểm có \(1 \lt N \le 5000\) và \(1 \lt M \le 20000\)
• 50% test ứng với 50% số điểm có \(1 \lt N, M \le 10^6\)

Input 1

6 12
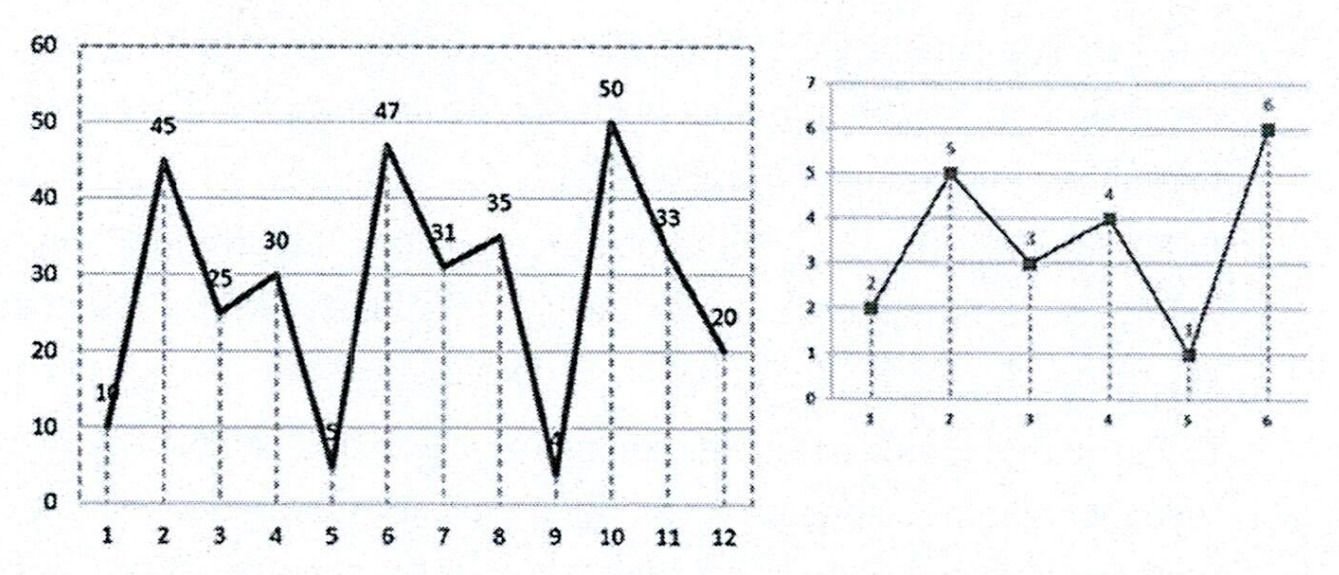
2 5 3 4 1 6
10 45 25 30 5 47 31 35 4 50 33 20

Output 1

2
1 5